Les Mongueurs de Perl / Groupe de travail Articles / Conférences Perl

Nous rejoindre / SVN / Relecture / Rédaction / Planning / Liens /

Publications : Linux Magazine France, Perles, Brèves, Production, Comptes-Rendus, Interviews, Traductions, Spoofathon

• directives

  afficher les déplacements à effectuer par le joueur. Par exemple :

      de 1 vers 3
      de 1 vers 2
      de 3 vers 2
      de 1 vers 3
      de 2 vers 1
      de 2 vers 3
      de 1 vers 3

• ASCII Art

  afficher une animation en art ASCII présentant les déplacements des disques, de

         =!=       !        !    
        ==!==      !        !    
       ===!===     !        !

  à

          !        !       =!=   
          !        !      ==!==  
          !        !     ===!===

• GUI

  afficher l'animation dans une interface graphique.

Chaque programme devait prendre le nombre de disques en paramètre sur la ligne de commande. Certains prennent la valeur 3 par défaut, mais si l'un des programmes ne fonctionne pas comme vous vous y attendez, commencez par fournir un paramètre au script en question.

Sans plus attendre, voici les résultats :

    sub _{$_[3]&&_(@_[0,2,1],$_[3]-1)&&_(@_[0..2],0)&&(@_[1,0
    ,2],$_[3]-1)||print"de $_[0] vers $_[2]\n"}_ 1..3,pop||2

Christophe Grosjean a travaillé sur une solution à base d'expressions régulières :

    #!/usr/bin/perl -l
    $_=123;for$a(1..pop){s/(\d)(\d)(\d)/$1$3$2de $1 vers $3
    $2$1$3/g};s/\d{3}//g;print

Notez l'utilisation du saut de ligne directement dans la chaîne pour gagner un précieux caractère...

Christophe s'est également fendu d'une version de l'algorithme itératif :

    printf"de %d vers %d\n",map{($_%3^(3)[$r&1])%3+1}($_&$_-1,($_|$_-1)+1)for 1..2**($r=pop)-1

Une mention spéciale pour Jérôme Quelin, qui a fait le programme le plus court. Pour un nombre de disques impair, il déplace la tour de la première aiguille à la troisième, alors que pour un nombre de disques pair, la solution mène la tour sur l'aiguille du milieu.

    #!/usr/bin/perl -l
    print"de ".(($_&$_-1)%3+1)." vers ".((($_|$_ -1)+1)%3+1)for 1..(1<<pop)-1

Jérôme est également l'auteur de versions encore plus courtes, que je n'ai pas pu intégrer faute de temps.

    $n=shift||3;$p=$"x($n+1);$e="$p!$p";substr($c=$p,0,$_,"="x$_),push@{$h[0]}
    ,join"!","".(reverse$c),$c for reverse 1..$n;print$h="\e[H\e[J$/",map{$_,
    $e,$e,$/}reverse@{$h[0]};sub _{$_[3]&&_(@_[0,2,1],$_[3]-1)&&_(@_[0..2],0
    )&&_(@_[1,0,2],$_[3]-1)||&O}sub O{select$,,$,,$,,1/$n;push@{$h[$_[2]]},
    pop@{$h[$_[0]]};print$h,map{$h[0][$ _]||$e,$h[1][$_]||$e,$h[2][$_]||$e
    ,$/}reverse 0..$n-1}_ 0..2,$n-1

Jean Forget, secrétaire perpétuel de Paris.pm, fait une proposition longue, qui rentre dans deux catégories à la fois, en fonction des options de ligne de commande qui lui sont passées (les options sont traitées par le paramètre -s de perl :

• l'option -d affiche les directives,

• l'option -g donne un affiche en ASCII Art.

    #!/usr/bin/perl -s
    use strict;
    use vars qw/$d $g/;

    my $n = $ARGV[0];
    my $ld = 2 * $n  + 1;
    my $l  = 3 * $ld;
    my $ll = $l + 1;

    my %s = qw/12 3 13 2 21 3 23 1 31 2 32 1/;
    @s{qw/1 2 3/} = $n % 2 ? qw/3 1 2/ : qw/2 3 1/;

    my ($j, $k, $v) = map { $_ x $n } ("1", "3", " ");

    sub aff {
      sleep 1;
      print "\e[H\e[J" if $g;
      printf "de %d vers %d\n", @_ if $d && @_;
      return unless $g;
      my $w = "$v|$v";
      my $a = "$w$w$w\n" x $n . "X" x $l;
      my $p = - $ld;
      foreach (split '', $j)
        {
          $w =~ s/ ([=|]+) /=$1=/;
          substr($a, $p + $_ * $ld, $ld) = $w;
          $p += $ll;
        }
      local $_ = "$a\n";
      1 while s/=(.{$l}) / $1=/gso;
      print;
    }
    sub impair {
      $j =~ s/^(.)/$s{$1}/;
      aff $1, $s{$1};
    }
    sub pairimp {
      $j =~ s/^(.)(\1*)(.)/$1$2$s{"$1$3"}/;
      aff $3, $s{"$1$3"};
      impair;
    }

    aff;
    impair;
    pairimp while $j ne $k;

Si on passe les deux options au programme, il affiche la solution dans les deux modes en simultané. Et si on ne lui passe aucune option ? Eh bien le script résout le problème pour lui tout seul et n'affiche rien. Na !

    $n=pop;use Tk;$m=new MainWindow;@s=([reverse 1..$n],[],[]);sub z{$m->
    title(pop)}push(@f,$f=$m->Frame->pack(side,left,fill,"y")),$f->Button
    (text,$_,width,4*$n,command,[sub{$z=pop;if(!$s){return$s[$z-1][-1]?z(
    $s=$z):0}return z($s="")if$s==$z--;return if$s[$z][-1]&&$s[$s-1][-1]>
    $s[$z][-1];(pop@{$b[$s-1]})->packForget;push@{$s[$z]},$w=pop@{$s[$s-1
    ]};push@{$b[$z]},$f[$z]->Button(width,3*$w)->pack(side,bottom);z($s=""
    )},$_])->pack(side,bottom)for 1..3;push@{$b[0]},$f[0]->Button(width,3
    *$_)->pack(side,bottom)for@{$s[0]};push@b,[],[];z("");MainLoop

Voici un aperçu du résultat :

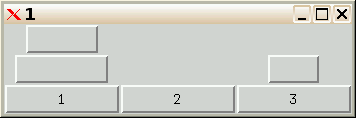
Il ne résout pas le problème, c'est à vous de le faire en cliquant sur les boutons 1, 2 et 3. Voici une bonne manière de vérifier que les autres programmes de cet article fonctionnent.

Maintenant que vous avez pris goût au déplacement des disques sur les aiguilles, vous pouvez aller visiter une partie du site de Amit Singh dédiée uniquement aux tours de Hanoï, dans divers langages de programmation : Hanoimania!, à l'adresse http://www.kernelthread.com/hanoi/.

Copyright © Les Mongueurs de Perl, 2001-2011 pour le site.
Les auteurs conservent le copyright de leurs articles.